Descubre cómo calcular el sentido de un vector de forma sencilla

El cálculo del sentido de un vector es un concepto fundamental en el campo de las matemáticas y la física. Un vector es una magnitud que tiene tanto magnitud como dirección, y su sentido es crucial para comprender su comportamiento y su aplicación en diversas disciplinas científicas. En este artículo, exploraremos en detalle cómo se calcula el sentido de un vector, así como las diferentes técnicas y fórmulas utilizadas para su determinación. Además, analizaremos ejemplos prácticos que ilustrarán la importancia y la utilidad de comprender y calcular correctamente el sentido de un vector en diferentes contextos.

• El sentido de un vector se calcula mediante la dirección en la que apunta. Para determinar el sentido, se debe observar hacia dónde se dirige la flecha que representa al vector.
• En castellano, el sentido de un vector se puede expresar utilizando palabras como "hacia arriba", "hacia abajo", "hacia la izquierda", "hacia la derecha", "hacia el norte", "hacia el sur", "hacia el este", "hacia el oeste", entre otros. Estas indicaciones ayudan a describir la orientación del vector en relación a un punto de referencia.

Ventajas

• Permite determinar la dirección de un vector: Al calcular el sentido de un vector, podemos identificar hacia dónde apunta. Esto es especialmente útil en física y geometría, ya que nos permite comprender la dirección de fuerzas o desplazamientos en un espacio determinado.
• Ayuda a realizar operaciones vectoriales: Al conocer el sentido de un vector, podemos realizar operaciones como sumas, restas o productos vectoriales de forma más precisa. Esto es esencial en campos como la física, la ingeniería o la navegación, donde se requiere realizar cálculos y análisis vectoriales para resolver problemas y tomar decisiones.

Desventajas

• Complejidad matemática: El cálculo del sentido de un vector puede resultar complicado para aquellos que no están familiarizados con los conceptos matemáticos y las fórmulas utilizadas en el álgebra vectorial. Requiere un conocimiento profundo de las operaciones y propiedades de los vectores.
• Dificultad de visualización: A veces, resulta difícil visualizar el sentido de un vector en el espacio tridimensional. A diferencia de la magnitud de un vector, que puede representarse fácilmente mediante una escala o una longitud, el sentido implica una dirección específica en el espacio, lo que puede resultar confuso para algunas personas.
• Dependencia del sistema de referencia: El sentido de un vector está intrínsecamente ligado al sistema de referencia utilizado para su cálculo. Cambiar el sistema de coordenadas puede alterar drásticamente el sentido de un vector, lo que puede llevar a confusiones o errores si no se tiene en cuenta esta dependencia. Esto puede resultar especialmente problemático cuando se trabaja en diferentes contextos o sistemas de coordenadas.

¿Cuál es la dirección y sentido de un vector?

La dirección y sentido de un vector son conceptos fundamentales en el estudio de las magnitudes vectoriales. La dirección se refiere a la orientación de un vector en el espacio, y está determinada por la recta de acción sobre la cual se encuentra el vector. Por su parte, el sentido indica hacia qué lado de la recta actúa el vector. Estos dos elementos son esenciales para comprender y representar correctamente los vectores en diversos contextos, como la física, la geometría o la ingeniería.

El estudio de las magnitudes vectoriales requiere comprender la dirección y sentido de los vectores. La dirección se determina por la recta de acción, mientras que el sentido indica hacia qué lado actúa el vector. Estos conceptos son esenciales en disciplinas como la física, geometría e ingeniería.

¿De qué manera se puede medir u obtener la dirección de un vector?

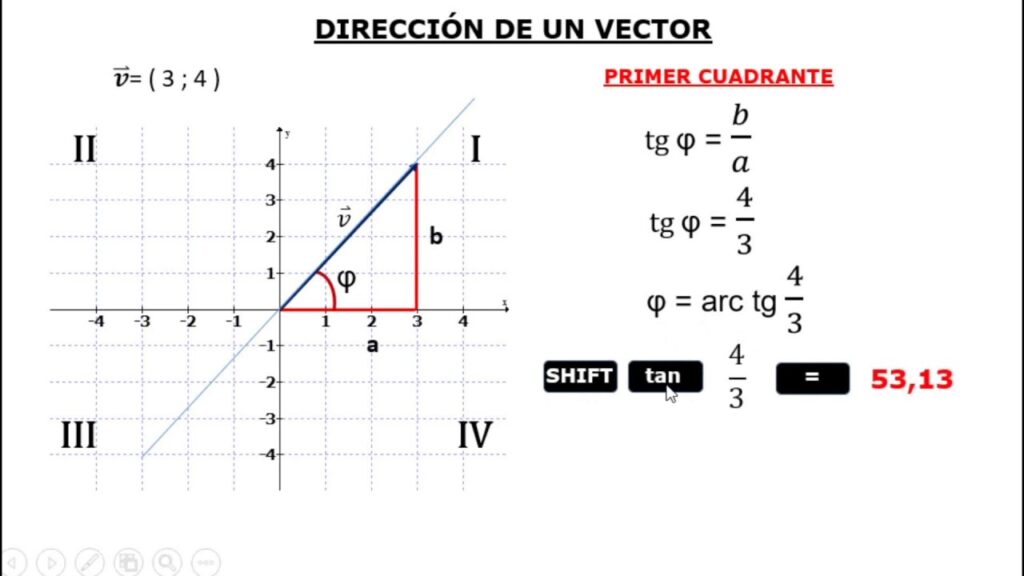
La dirección de un vector se puede medir u obtener calculando la tangente inversa del componente en y del vector sobre el componente en x. Este método es válido para vectores en un sistema de coordenadas 2D. La dirección se expresa generalmente mediante el ángulo que forma el vector con uno de los ejes del sistema de coordenadas.

Calcular la dirección de un vector en un sistema de coordenadas 2D es posible utilizando la tangente inversa del componente en y sobre el componente en x. Esta medida se expresa comúnmente mediante el ángulo formado entre el vector y uno de los ejes del sistema de coordenadas.

¿Cuál es la fórmula para calcular la magnitud de un vector?

La fórmula para calcular la magnitud de un vector es bastante sencilla. Se trata de calcular la raíz cuadrada de la suma de los cuadrados de sus componentes. Por ejemplo, si tenemos un vector con componentes a y b, la magnitud se obtiene al calcular la raíz cuadrada de a al cuadrado más b al cuadrado. Esto nos da una medida de la longitud o tamaño del vector en el espacio. En resumen, la fórmula para calcular la magnitud de un vector es la raíz cuadrada de a al cuadrado más b al cuadrado.

La magnitud de un vector se calcula mediante la raíz cuadrada de la suma de los cuadrados de sus componentes. Esta fórmula nos proporciona una medida de la longitud o tamaño del vector en el espacio. En resumen, la magnitud de un vector se obtiene a partir de la raíz cuadrada de la suma de los cuadrados de sus componentes.

El cálculo del sentido de un vector: una guía paso a paso

El cálculo del sentido de un vector es una tarea fundamental en las matemáticas y la física. Para determinar el sentido de un vector, es necesario seguir una serie de pasos. En primer lugar, se debe identificar el punto de inicio y el punto de llegada del vector. Luego, se traza una línea recta desde el punto de inicio hasta el punto de llegada. El sentido del vector se determina por la dirección de esta línea recta, es decir, si va de izquierda a derecha, de arriba a abajo, etc. En resumen, el cálculo del sentido de un vector requiere un análisis cuidadoso de su trayectoria.

Es importante destacar que el sentido de un vector no solo se determina por la dirección de la línea recta, sino también por el contexto en el que se encuentra. Por ejemplo, en física, el sentido de un vector puede indicar si se trata de una fuerza hacia adelante o hacia atrás, lo cual es crucial para comprender el movimiento de un objeto. En conclusión, el cálculo del sentido de un vector es esencial para el análisis matemático y físico, ya que nos brinda información clave sobre su trayectoria y su impacto en los sistemas en los que se aplica.

Descifrando el sentido de un vector: métodos y fórmulas clave

Entender el sentido de un vector es fundamental en el ámbito matemático y físico. Para ello, se utilizan diferentes métodos y fórmulas clave. Uno de los métodos más comunes es la regla de la mano derecha, donde se utiliza el pulgar, el índice y el dedo medio para determinar la dirección del vector. Además, existen fórmulas matemáticas como la suma y la resta de vectores, así como el producto escalar y el producto vectorial, que permiten analizar y calcular el sentido de un vector de manera precisa. Estas herramientas son indispensables para comprender y resolver problemas relacionados con vectores en diversas disciplinas científicas.

De la regla de la mano derecha, la suma, resta, producto escalar y producto vectorial son fórmulas esenciales para comprender y calcular el sentido de un vector en matemáticas y física. Estas herramientas son fundamentales para resolver problemas en diferentes disciplinas científicas.

Explorando el sentido de un vector: conceptos fundamentales y aplicaciones prácticas

En el campo de la física y las matemáticas, el sentido de un vector juega un papel crucial. Un vector es una magnitud que tiene dirección y magnitud, y su sentido indica la dirección en la que se mueve. Además, el sentido de un vector puede ser utilizado para calcular fuerzas, velocidades y desplazamientos en diferentes campos de la ciencia. En este artículo exploraremos los conceptos básicos del sentido de un vector y su importancia en diversas aplicaciones prácticas.

El sentido de un vector es esencial en la física y las matemáticas, ya que indica la dirección en la que se mueve una magnitud. Su importancia radica en que permite calcular fuerzas, velocidades y desplazamientos en distintos campos científicos.

Determinando la dirección de un vector: técnicas esenciales y ejemplos resueltos

Determinar la dirección de un vector es fundamental en el ámbito de las matemáticas y la física. Existen varias técnicas para lograrlo, como el uso de coordenadas polares o la aplicación de trigonometría. En este artículo, exploraremos estos métodos y presentaremos ejemplos resueltos para facilitar la comprensión. Aprender a determinar la dirección de un vector nos permitirá resolver problemas de manera más eficiente y precisa en diversas disciplinas científicas.

De las técnicas mencionadas, también se puede determinar la dirección de un vector utilizando el método de las componentes cartesianas. Este método consiste en descomponer el vector en sus componentes en los ejes x e y, y luego utilizar trigonometría para obtener el ángulo de dirección. A través de este enfoque, se puede obtener una comprensión más completa y precisa de la dirección de un vector en el espacio.

Descubre cómo determinar el sentido de un vector de forma sencilla

¡Aprende fácilmente cómo determinar el sentido de un vector con estos simples pasos! Utilizando reglas y fórmulas básicas, podrás identificar la dirección correcta de cualquier vector en cuestión de minutos. ¡No te pierdas este tutorial para dominar este concepto fundamental de la física!

Descubre cómo calcular el sentido de un vector de manera fácil y precisa

Si estás buscando cómo calcular el sentido de un vector de forma sencilla, has llegado al lugar indicado. En matemáticas, el sentido de un vector se determina por la dirección en la que apunta. Para calcularlo, simplemente necesitas conocer las coordenadas del vector y aplicar la fórmula adecuada. Con nuestra guía paso a paso, aprenderás a calcular el sentido de un vector de manera fácil y rápida. ¡No te pierdas esta oportunidad de dominar este concepto importante!

Descubre el significado del sentido en un vector

¿Te has preguntado qué es el sentido en un vector? Descubre cómo calcularlo de forma sencilla con nuestra guía paso a paso. El sentido en un vector se refiere a la dirección en la que se mueve, y es crucial para comprender su magnitud y orientación. Con nuestros consejos, podrás determinar fácilmente el sentido de un vector y aplicarlo en tus cálculos matemáticos. ¡No esperes más y aprende todo sobre el sentido en un vector ahora!

Domina el arte de calcular la dirección y sentido de un vector

Calcular la dirección y sentido de un vector es fundamental en matemáticas y física. Para hacerlo de forma sencilla, primero debes identificar las coordenadas del vector en un plano cartesiano. Luego, puedes determinar su dirección utilizando la tangente inversa de la componente y sobre la componente x. El sentido del vector se determina observando si es positivo o negativo en cada componente. ¡Descubre cómo calcularlo de manera fácil y precisa!

Descubriendo la dirección de un vector

Para determinar el sentido de un vector de forma sencilla, simplemente se debe observar la dirección en la que apunta la flecha que representa al vector. Si la flecha va de un punto A a un punto B, el sentido del vector es de A hacia B. Es importante recordar que el sentido de un vector es crucial en física y matemáticas para interpretar correctamente sus magnitudes y operaciones.

En resumen, el cálculo del sentido de un vector es fundamental en el ámbito de las matemáticas y la física, ya que permite determinar la dirección en la que se desplaza dicho vector. Para ello, se utilizan diversos métodos y fórmulas, dependiendo del tipo de vector y las variables involucradas. Es importante tener en cuenta que el sentido de un vector no se puede expresar únicamente en términos de magnitud, sino que también debe considerarse la orientación en relación a un sistema de referencia establecido. Además, es necesario conocer los conceptos básicos de álgebra vectorial y geometría para comprender y aplicar correctamente las fórmulas de cálculo del sentido de un vector. En conclusión, el cálculo del sentido de un vector es una herramienta fundamental en diversas disciplinas científicas y su correcta determinación contribuye a un análisis más preciso y completo de los fenómenos físicos y matemáticos.