Descubre la Notación y Clasificación de Triángulos: Definición Completa en 70 Caracteres.

Los triángulos son una de las formas más básicas de la geometría euclidiana, y son fundamentales en muchos campos de las matemáticas y la física. La definición más común de un triángulo es una figura plana de tres lados y tres ángulos, pero esta es solo el comienzo de una discusión más completa. En este artículo especializado, nos adentraremos en la notación y clasificación de los triángulos, desde los distintos tipos de triángulos según sus ángulos y lados hasta las diferentes formas de representarlos en términos matemáticos. Con esta información, esperamos brindar una comprensión más profunda y completa de estos polígonos básicos, y su relevancia en el mundo de las matemáticas y la física.

Ventajas

• 1) Clasificar los triángulos permite entender mejor sus propiedades y características únicas. Por ejemplo, los triángulos isósceles tienen dos lados iguales y dos ángulos iguales, lo que significa que también tienen simetría axial en su eje perpendicular al lado desigual. Esta información puede ser útil en la geometría, la construcción de estructuras y la resolución de problemas matemáticos.
• 2) La notación y definición de triángulos también facilita la comunicación matemática entre profesores y estudiantes, así como entre profesionales en campos como la arquitectura, la ingeniería y la física. Al tener un lenguaje común para hablar sobre triángulos, se puede evitar confusiones y errores en los cálculos y diseños. Además, los nombres de los diferentes tipos de triángulos a menudo se utilizan en otros contextos, lo que permite a los estudiantes aplicar y transferir su conocimiento de la geometría a otras disciplinas.

Desventajas

• Complejidad: La definición y notación de triángulos puede ser compleja y difícil de entender para aquellos que no tienen experiencia en la geometría. La clasificación de triángulos en diferentes tipos según sus atributos también puede resultar confusa.
• Dificultad de identificación: La clasificación puede volverse complicada cuando los atributos son similares. Identificar la diferencia entre un triángulo escaleno y uno isósceles, por ejemplo, puede requerir un gran esfuerzo y atención a los detalles.
• Limitación: La definición y notación de triángulos se limita a las figuras bidimensionales. Por lo tanto, no puede describir relaciones tridimensionales o de formas irregulares que no se puedan identificar fácilmente como triángulos.
• Redundancia: En algunos casos, la definición y notación de los triángulos tiene un alcance limitado o no es necesaria para realizar cálculos o resolver problemas. Puede haber otros métodos más eficientes para describir y clasificar un triángulo en función de sus atributos.

¿Cuál es la definición, la notación y la clasificación?

La notación matemática es el sistema de símbolos utilizado para representar conceptos y operaciones en el lenguaje formal de las matemáticas. La notación se utiliza para comunicar ideas y soluciones de una manera concisa y precisa. Hay diferentes tipos de notación matemática, como la notación alfabética, la notación numérica y la notación simbólica. La notación simbólica es común en áreas como la álgebra, la geometría y el cálculo, y utiliza símbolos específicos para representar conceptos matemáticos complejos. La notación matemática es esencial para la comunicación efectiva en el campo de las matemáticas.

La notación matemática es el sistema de símbolos utilizado para comunicar conceptos y operaciones de manera concisa y precisa en las matemáticas. La notación simbólica es común y esencial para áreas como la álgebra, la geometría y el cálculo. La notación matemática es fundamental para la comunicación efectiva en el campo de las matemáticas.

¿Cuál es la definición de la notación de un triángulo?

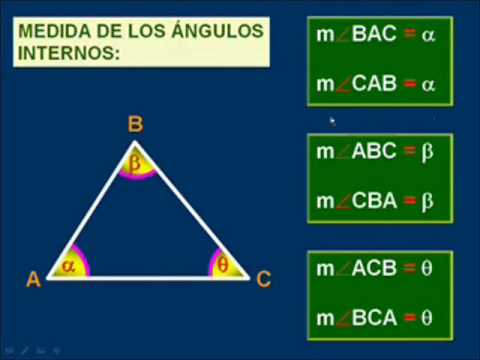
En la geometría, la notación de un triángulo es un conjunto de símbolos que se utilizan para designar los lados y vértices de un triángulo específico. Este sistema de notación se utiliza para simplificar las fórmulas y ecuaciones que se utilizan para resolver problemas relacionados con triángulos. En particular, se utilizan las letras 'a', 'b' y 'c' para designar los lados de un triángulo, mientras que las letras 'A', 'B' y 'C' se refieren a los vértices correspondientes. En general, esta notación ayuda a los matemáticos a trabajar con mayor precisión y eficiencia cuando se trata de problemas de geometría.

La notación de un triángulo es un conjunto de símbolos utilizados para designar lados y vértices. Las letras 'a', 'b' y 'c' se usan para los lados, y 'A', 'B' y 'C' para los vértices. Esta notación ayuda a los matemáticos a resolver problemas geométricos de manera más precisa y eficiente.

¿Cuál es la definición de triángulos y cómo se clasifican?

El triángulo es una figura plana formada por tres lados y tres ángulos. Según sus lados, se clasifican en tres tipos: el triángulo equilátero, que tiene sus tres lados y tres ángulos iguales; el triángulo isósceles, que tiene dos lados y dos ángulos iguales, mientras que el tercer lado y angulo son distintos; y finalmente, el triángulo escaleno, el cual tiene sus tres lados y tres ángulos diferentes. Es importante conocer los diferentes tipos de triángulos para poder aplicar los diferentes teoremas y fórmulas correspondientes en el análisis de figuras geométricas.

Los triángulos son figuras planas que se clasifican en tres tipos según sus lados: equilátero, isósceles y escaleno. El conocimiento de los diferentes tipos de triángulos es fundamental para la aplicación correcta de fórmulas y teoremas en el análisis de figuras geométricas.

La importancia de conocer la definición, notación y clasificación de los triángulos

La comprensión de la definición, notación y clasificación de los triángulos es crucial en el estudio de la geometría. El conocimiento detallado de estas características puede ayudar a distinguir entre diferentes tipos de triángulos y resolver problemas geométricos de manera más eficiente. Además, esta información resulta útil en la aplicación práctica, como por ejemplo en la construcción de edificios u objetos con formas triangulares. Al conocer las propiedades de los triángulos, se pueden evitar errores comunes y garantizar una precisión en el diseño y construcción de estructuras geométricas.

La comprensión y diferenciación de los tipos de triángulos es esencial en geometría y en aplicaciones prácticas de construcción. Conocer sus propiedades permite evitar errores comunes y garantizar precisión en el diseño y construcción de estructuras triangulares.

Explorando la diversidad de triángulos: una guía para entender su notación y clasificación

Los triángulos son una de las figuras geométricas más comunes y versátiles en la matemática. Sin embargo, a menudo se subestima su riqueza y variedad, lo que lleva a una comprensión incompleta de su comportamiento en diferentes situaciones. Para entender mejor los triángulos, es necesario comprender su notación y clasificación. En este artículo, exploraremos los diferentes tipos de triángulos y las diferentes formas en que se pueden clasificar. Desde la notación básica hasta las propiedades más complejas, esta guía proporcionará una introducción completa a la diversidad de triángulos.

Esta guía proporciona una comprensión completa de la diversidad y clasificación de los triángulos, desde la notación básica hasta las propiedades complejas. Es importante entender su riqueza y versatilidad para comprender su comportamiento en diferentes situaciones. Exploraremos los diferentes tipos de triángulos y sus clasificaciones.

Los triángulos son figuras geométricas fundamentales que se utilizan en muchas disciplinas, desde la física hasta la arquitectura y la ingeniería. La comprensión de los diferentes tipos de triángulos, su notación y clasificación es esencial para cualquier estudiante de matemáticas. Los triángulos se pueden clasificar de diferentes maneras en función de sus lados y ángulos, lo que proporciona una base sólida para la resolución de problemas y aplicaciones en el mundo real. Al entender los conceptos básicos de los triángulos, se sientan las bases para un mayor conocimiento en el campo de la geometría, lo que puede ser útil en una amplia variedad de situaciones. En resumen, la definición, notación y clasificación de los triángulos son una parte fundamental del estudio de la geometría, y su conocimiento es esencial para cualquier persona que desee comprender la matemática en un nivel avanzado.